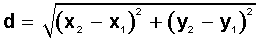2) LÍNEA RECTA

Empecemos definiendo teóricamente a una recta como una sucesión infinita de puntos que tiene una única inclinación y también única pendiente.

Entonces, para identificar claramente a una recta y asegurar que es única en cuanto a su expresión matemática o fórmula, se deben tener en conocimiento necesariamente dos datos:

             - Dos puntos de la recta ó
             - Un punto de la recta y su pendiente ó
             - Un punto de la recta y su inclinación.

Vayamos viendo cómo podemos calcular la ecuación de la recta en cada uno de los casos mencionados anteriormente:

ECUACIÓN DE LA RECTA CONOCIDOS DOS DE SUS PUNTOS:

Teniendo 2 puntos conocidos en el plano que pasen por la recta buscada, se puede afirmar que solamente una recta pasará por esos 2 puntos, es decir, la recta que pase por esos 2 puntos será única y no existirá otra recta diferente con esas características.

Si tomamos tres puntos pertenecientes a una recta, dos de ellos conocidos A(x1, y1) y B(x2, y2), y un punto (x, y) cualquiera desconocido, se puede encontrar la ecuación cartesiana de la recta conocidos dos puntos donde el primer punto será A(x1, y1) y el segundo punto será B(x2, y2) con la siguiente expresión:

ECUACIÓN DE LA RECTA CONOCIDOS UN PUNTO Y SU PENDIENTE:

Otra forma para afirmar y confirmar que sólo una recta pasará por un punto conocido es conocer también su pendiente, es decir, si conocemos un punto cualquiera de la recta y también su pendiente, podemos afirmar que sólo una recta tendrá esa pendiente y pasará por ese punto:

Donde (x1, y1) es el punto conocido y m es su pendiente

ECUACIÓN DE LA RECTA CONOCIDOS UN PUNTO Y SU INCLINACIÓN:

Si se desea trabajar con el ángulo de inclinación, recordemos que la pendiente es igual a la tangente del ángulo de inclinación, lo que hace que la expresión sea la siguiente:

Donde (x1, y1) es el punto conocido y α es su ángulo de inclinación.

ORDENADA EN EL ORÍGEN – PENDIENTE:

Cuando se conocen la pendiente de la recta y la intersección de la misma con el eje y:

donde m es la pendiente y b es la intersección con el eje y

ECUACIÓN GENERAL DE LA RECTA

La ecuación general de la recta puede adoptar la forma general:

Ax + By + C = 0

Donde los coeficientes A y B nos ayudan a determinar la pendiente de la recta y, está dada por la siguiente expresión:

Pendiente m = - A/B

También podemos aprovechar los coeficientes B y C que nos ayudan a determinar el punto de intersección de la recta con el eje de las ordenadas (y).

Intersección recta con ordenada en el origen = - C/B

En general, partiendo de la ecuación cartesiana de la recta podemos llegar a expresar o nombrar a la recta única de forma general que es la forma más utilizada para la resolución de problemas de carácter económico – administrativo, es decir:

Si queremos encontrar la ecuación de la recta en su forma general que pasa por los puntos A(1,2) y B(2,-3) aplicando la ecuación de la recta que pasa por dos puntos tenemos:

De donde la pendiente será igual a -A/B = -5/1 ó -5

Y la intersección con el eje y será igual a -C/B = -(-7)/1 ó 7

Si queremos encontrar la misma ecuación expresada en la forma expresada en el origen pendiente tenemos que despejar y:

y = -5x +7

donde la pendiente m es -5 y la intersección con el eje y b es 7

PARALELISMO:

Dos o más rectas son paralelas si sus pendientes o sus ángulos de inclinación son iguales, es decir:

m1 = m2         ó         α1 = α2

Si queremos hallar la recta paralela a 5x+2y-3=0 que pase por el punto (1,4):

La pendiente de la recta de referencia es -5/2 que también es la pendiente de la recta buscada.

Con m = -5/2 y el punto (1,4)

Reemplazamos en la ecuación de la recta:     y - 4 = - 5/2 ( x - 1 )

Realizando operaciones aritméticas:       2y - 8 = -5x + 5

La ecuación buscada será:        5x + 2y - 13 = 0

Que es paralela a 5x+2y-3=0 y pasa por el punto (1,4)

PERPENDICULARIDAD:
Para que dos rectas sean perpendiculares, la pendiente de una de ellas debe ser inversa y de signo contrario de la otra, es decir:

                                                                     m1 = - 1/m2

Si queremos hallar la recta perpendicular a 5x+2y-3=0 y que pase por el punto (1,4):

La pendiente de la recta de referencia es -5/2, entonces la pendiente de la recta buscada será 2/5.

Con m = 2/5 y el punto (1,4)

Reemplazamos en la ecuación de la recta:     y - 4 = 2/5 ( x - 1 )

Realizando operaciones aritméticas:       5y - 20 = 2x - 2

La ecuación buscada será:          2x - 5y + 18 = 0

Que es perpendicular a 5x+2y-3=0 y pasa por el punto (1,4)

APLICACIÓN DE LA LINEA RECTA EN PROBLEMAS DE CARÁCTER ECONÓMICO – ADMINISTRATIVO:

Análisis del Mercado: Oferta, Demanda y Punto de Equilibrio

Antes de analizar este fenómeno económico es necesario definir algunos conceptos:

MERCADO: Lugar (puede ser físico o no) donde compradores y vendedores hacen negocios entre sí con ciertos conocimientos e información de los productos (precio), los compradores son los demandantes y los vendedores son los ofertantes.

DEMANDA: Cantidad de bienes y/o servicios que los consumidores están dispuestos a adquirir a un precio determinado y en un momento dado. La ley de la demanda nos indica que existe una relación inversamente proporcional entre el precio y la cantidad demandados, es decir que si el precio baja, la cantidad demandada sube; y si el precio sube, la cantidad demandada baja.
Entonces es correcto interpretar el comportamiento de la demanda desde el punto de vista de los compradores o consumidores de bienes y/o servicios y además considerar que por su comportamiento la demanda siempre tendrá geométricamente pendiente negativa.

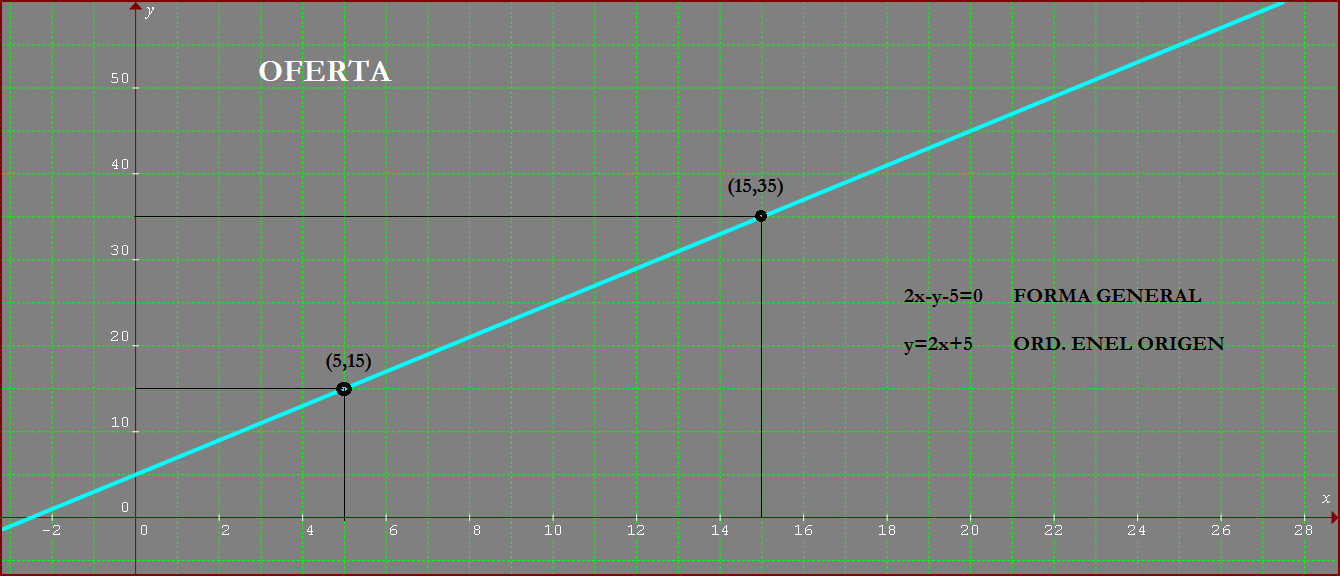
OFERTA: Cantidad de bienes y/o servicios que los productores o distribuidores están dispuestos a ofrecer en un mercado a un precio determinado y en un momento dado. La ley dela oferta nos indica que existe una relación directamente proporcional entre el precio y la cantidad ofertados, es decir que si el precio baja la cantidad ofertada también bajará, y si el precio sube, la cantidad ofertada subirá.
Entonces debemos interpretar el comportamiento de la oferta desde el punto de vista de los productores, distribuidores de productos o prestadores de servicios y además se debe considerar que por su comportamiento, la oferta siempre tendrá geométricamente pendiente positiva.

EQUILIBRIO DE MERCADO: Precio y cantidad donde demandantes y ofertantes (consumidores y productores) están de acuerdo, geométricamente ambos están en un mismo punto en común, es decir cuando las rectas (o curvas) de demanda y oferta se interceptan.

Ejemplo: Un estudio de mercado demuestra que si el precio de un producto es de 200 $/unidad se demandarán 8000 unidades y los productores pondrían en el mercado 15000 unidades. Pero si el precio baja a 160 $/unidad, los productores pondrían en el mercado 7000 unidades pero los consumidores estarían dispuestos a adquirir 10000 unidades.
Determine las ecuaciones de la oferta y demanda, además de determinar el punto de equilibrio de mercado, adicionalmente, que pasará si el precio final del producto en el mercado llega a ser 190 $?

Solución: Podemos empezar identificando los datos del problema y podemos realizar un cuadro que pueda resumir ello:

A continuación determinamos las ecuaciones de la Demanda y Oferta considerando la ecuación de la recta para cada caso:

Teniendo las ecuaciones de oferta y demanda podemos calcular el punto de equilibrio del mercado resolviendo el sistema de 2 ecuaciones con 2 incógnitas (para ello por el caso solucionamos por sustitución):

El punto de equilibrio de mercado está en el punto (9400, 172).

Para analizar lo que ocurre si el precio de venta es de 190 $/unidad, es necesario encontrar los puntos tanto de oferta como de demanda que obviamente no están en el punto de equilibrio, sino un poco por encima y cada uno de ellos nos muestra una demanda y oferta diferentes:

Análisis del Costo - Ingreso - Utilidad

El Costo Total en una empresa está dado por la ecuación:

CT = CV + CF        y         CV = CVu ∙ Q            se puede indicar que:

                        CT = CVu ∙ Q + CF           y...haciendo una analogía con la ecuación de la recta:

                          y  =    a      x   +    b 

Como se muestra en las anteriores ecuaciones, es posible analizar a los costos como una función lineal (línea recta) realizando una analogía con el cambio de variables de y a CT y de x a Q, que siguen siendo nuestras variables dependiente e independiente respectivamente.
El tratamiento que se le puede dar a este tipo de ecuación es como de cualquier línea recta con sus características particulares: pendiente, intersección con el eje y, etc. entonces, si se tiene por ejemplo en una empresa Costos Fijos de 2500 $, Costos Variable Unitario de 24 $/unid, la ecuación de Costo Total que representa este comportamiento será:

CT = 24 Q + 2500

Dentro de la empresa es sencillo obtener los datos de Costo Fijo o Costo Variable, pero se tiene también otra forma de cálculo empleando la ecuación de la línea recta conocidos dos puntos relacionando los Costos Totales con una determinada cantidad producida como sigue en el siguiente ejemplo: 

Si una empresa productora de pantalones al producir 200 unidades eroga costos por un valor de 30000 Bs., y luego al producir 300 unidades sus costos llegan a 40000 Bs., se pueden emplear esos datos para determinar su ecuación lineal de costo en las condiciones descritas anteriormente:

                                          Q1 = 200 Unid                  CT1 = 30000 Bs
                                          Q2 = 300 Unid                  CT2 = 40000 Bs

Entonces:

El Ingreso Total por ventas de los productos y/o servicios está dado por la ecuación:

IT=P∙Q

Donde se observa que el Ingreso Total depende del precio de venta asumido para poder analizar conjuntamente el CT.

La Utilidad en cualquier empresa está dada por la ecuación: U = IT – CT y se podrá relacionar ambos componentes para encontrar características e información importante que permitirá tomar decisiones importantes en las empresas.

Entonces, continuando con el ejemplo de los pantalones, asumamos que se adopta un precio de venta de 210 Bs./Unid., entonces tendremos:

IT=210 Q

Tenemos las ecuaciones de Ingreso y Costo para esta empresa:

Que nos permitirá determinar la ganancia o pérdida dependiendo del nivel de producción que se tenga.

Un dato importante para cualquier empresa es determinar el nivel de producción para no obtener ni ganancia ni pérdida, es decir que su utilidad sea = 0.

0 = 110 Q - 10000

Q = 10000/110 = 90.91 Unid.= 91 Unid.

Es decir que cuando esta empresa produzca 91 unidades de su producto no tendrá ni ganancia ni pérdida, esto convierte este importante dato en la primera meta que deberá buscar la empresa teniendo la seguridad de que si su nivel de producción sobrepasa las 91 unidades, es decir a partir de la unidad 92, la empresa tendrá utilidades y dependerá del nivel final de producción que tenga.

A continuación se presenta un ejercicio muy práctico donde se observa el comportamiento de estos conceptos en un problema de aplicación real:

UTILIDAD EN LAS EMPRESAS

1) CONCEPTOS BÁSICOS DE GEOMETRÍA ANALÍTICA

La Geometría Analítica puede considerarse una parte de la matemática que estudia todo elemento geométrico.

Por análisis se interpreta como la resolución de problemas y principalmente la interpretación de resultados.

Se destaca que la Geometría Analítica comienza en 1629 con Fermant, posteriormente Descartes en 1637 quien dio ímpetu al desarrollo de un enfoque algebraico sistemático y consistente para el estudio de la geometría. Cincuenta años más tarde, Newton y Leibniz empiezan con el Cálculo Diferencial e Integral.

Con todo lo anterior se puede acotar que no se hicieron muchos descubrimientos nuevos a los que estudiaron estos matemáticos años atrás, en lo que se mejoró fue en optimizar el trabajo de cálculo con el uso de tecnologías que al pasar el tiempo fueron facilitando más y más el trabajo: programas, máquinas, software, aplicaciones, etc.

Ya entrando a lo que nos concierne, en este tema veremos únicamente los conceptos (no todos) que nos servirán de base para más adelante en el análisis matemático de los fenómenos económicos recordando incluso la mayoría de ellos que ya fueron presentados anteriormente en la formación colegial o pre universitaria.

PLANO CARTESIANO: Está formado por dos rectas numéricas perpendiculares, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano tiene como finalidad describir la posición de puntos, los cuales se representan por sus coordenadas o pares ordenados.

Las coordenadas se forman asociando un valor del eje de las equis a uno de las yes, respectivamente, esto indica que un punto (P) se puede ubicar en el plano cartesiano tomando como base sus coordenadas, lo cual se representa como:

                   P (x, y)

Para localizar puntos en el plano cartesiano se debe llevar a cabo el siguiente procedimiento:

1. Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia la izquierda si son negativas, a partir del punto de origen, en este caso el cero.

2. Desde donde se localiza el valor de x, se cuentan las unidades correspondientes (en el eje de las ordenadas) hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas ambas coordenadas.

COORDENADAS CARTESIANAS: Las coordenadas cartesianas son pares de la forma (x, y) que generalmente son números reales, que representan un punto específico y único en el plano cartesiano. Los elementos reales se llaman pares ordenados.

Para el estudio de los fenómenos económicos una gran parte, por no decir todos, los ejercicios emplean el cambio de las variable, es así que veremos pares ordenados:

                   (q, p) Cantidad y Precio

                   (q, CT) Cantidad y Costo Total

                   (q, U) Cantidad y Utilidad

                   (t, U) Tiempo y Utilidad

Y así sucesivamente, empleando las coordenadas dependiendo del problema o fenómeno económico que se quiere analizar.

DISTANCIA ENTRE DOS PUNTOS: La distancia entre dos puntos ubicados horizontalmente paralelos al eje x (–4, 0) y (5, 0) es 5 – (–4) = 5 +4 = 9 unidades.

Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.

Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para hallar la distancia entre dos puntos en el plano teniendo las coordenadas de los puntos en cuestión, aplicamos el teorema de Pitágoras en el triángulo rectángulo.

Ejemplo:

INCLINACIÓN Y PENDIENTE DE UN SEGMENTO:
La inclinación de un segmento o una recta llega a ser el menor de los ángulos que dicha recta o segmento forma con el eje o semieje x positivo, se mide en grados desde el eje o semieje hacia la recta o segmento en sentido antihorario.

Si la recta es paralela al eje “y” su inclinación será por lógica 90° y si es paralela al eje “x” será 0°.

                                                 Inclinación = α = tan¯¹ ((y2-y1) / (x2-x1))

Por otro lado, la pendiente de un segmento o una recta es la tangente del ángulo de inclinación de la misma y llega a ser un número adimensional (sin unidades); desde el punto de vista geométrico se interpreta a la pendiente como la relación vertical versus horizontal de un segmento o una recta. Para calcular la pendiente se toma en cuenta ciertas condiciones y se toma en cuenta su signo, si la recta es paralela al eje “x” su pendiente vale 0 y si es paralela al eje “y” su pendiente es infinita (tan 90° = Infinito).

                                             m = tan α